Stochastic Simulation and Analysis

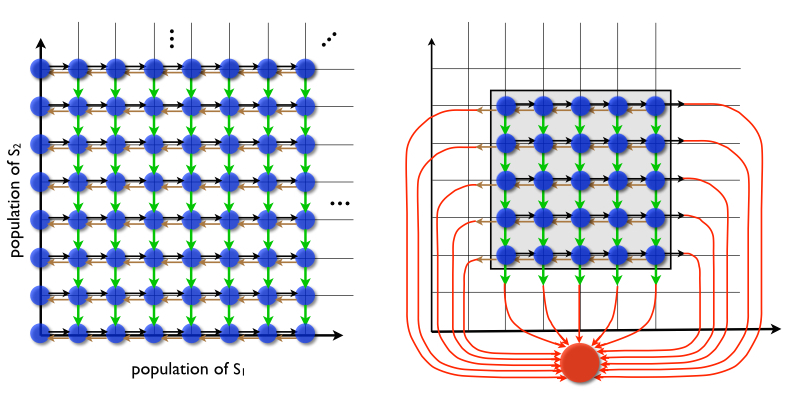
The Chemical Master Equation (CME), describes the time evolution of the joint probability density function of the various species being modeled in a stochastic chemically reacting system. We have been developing tools for the accurate solution of the CME.  The Finite State Projection method, which has been developed by the PI and his former studenty Munsky, provides a means for reducing the infinite CME into a finite linear system of equations. This system could be quite large, however, and one faces the curse of dimensionality when looking at larger problems. Recent work in collaboration with the Schwab group aims at overcoming the curse of dimensionality. It is based on the use of Quantized Tensor Train (QTT) formatted numerical linear algebra for the low parametric, numerical representation of tensors.

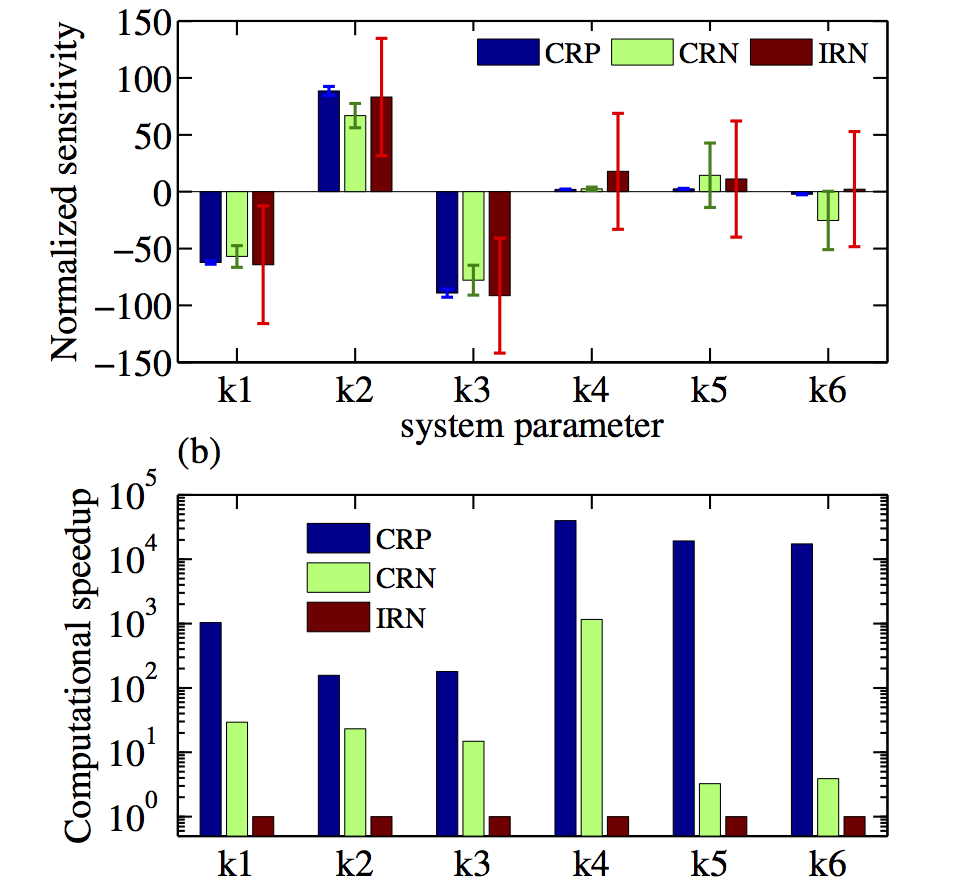
Models of biochemical reaction networks typically involve many kinetic parameters that influence their dynamic behavior. Sensitivity analysis is an indepsensible tool for their study and evaluation.  Such analysis quantifies the effect of changes in parameter values on an outcome of interest, giving insight into network design and its robustness properties. Sensitivity analysis is used to identify the important reactions for a given output, which can be used in experiment design and to identify potential targets for drug therapy. Finally sensitivity analysis can aid in the estimation of model parameters and in optimizing and fine-tuning the system’s behaviour in synethic circuit design. We have been developing very efficient computational tools and software for the sensitivity analysis of stochastic models of biochemical reaction networks. By exploiting different couplings of reaction trajectories, we are able to develop methods that are often orders of maganitude more efficient than what what was previously possible.

The existing sensitivity estimation methods become computationally infeasible for even moderately large networks because they rely on time-consuming Monte Carlo simulations of the exact reaction dynamics. Currently we are working towards eliminating this critical bottleneck by developing methods  that can accurately estimate parameter sensitivities using only approximate tau-leap simulations of the reaction dynamics. In the future we would like to combine such methods with multilevel strategies to gain computational efficiency and lower the approximation bias in the sensitivity estimator.

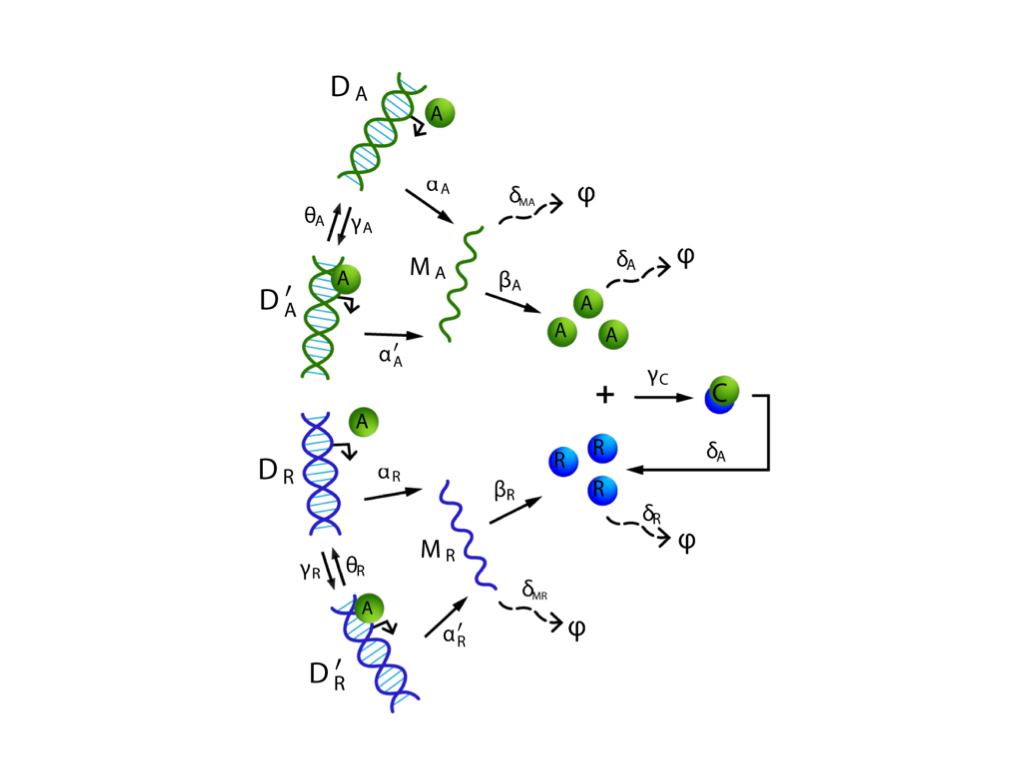
We have been developing a constructive scalable framework for examining the long-term behavior and stability properties of stochastic reaction dynamics. Specifically, we address the problem of determining ergodicity of the reaction dynamics, which is analogous to having a globally attracting fixed point for deterministic dynamics. The ergodicity properties of a process enable us to examine when the statistical moments of that process remain bounded over time and when they converge to their steady state values. The framework we develop relies on a blend of ideas from probability theory, linear algebra and optimization theory. Using this approach, we can show that the stability properties of a wide class of biological networks can be assessed using efficient and scalable linear programs, well-known for their tractability. The validity, efficiency, and wide applicability of these results can be demonstrated on several reaction networks arising in biochemistry, systems biology, epidemiology and ecology.

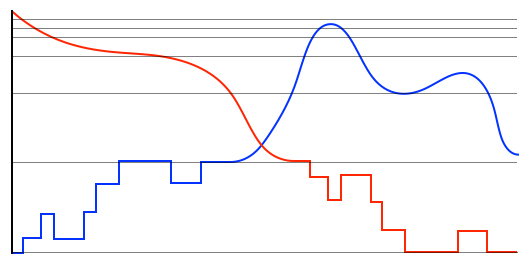
Hybrid methods for simulating a system of stochastically reacting species typically partition the set of species and set of reactions into discrete and continuous subsets, then rely on quasi-stationary assumptions to approximate the dynamics of fast subnetworks. As the dynamics evolve in time these partitions might have to be adapted during the simulation. We have recently been developing hybrid methods that automatically partition the reactions and species sets into discrete and continuous components, while applying dynamically the quasi-stationary assumption. Our methods do not require user intervention, as they exploit the changing timescale separation between reactions and/or changing magnitudes of copy-numbers of constituent species. Application to problems in Systems Biology show that very good approximations can be achieved in significantly less computational time. These tools are especially suitable for systems with oscillatory dynamics where the system dynamics change considerably throughout the time-period of interest.