Model and Parameter Inference
The living cell is abuzz with noise that manifests as stochastic fluctuations in a give cell over time. Consequently, clonal cell populations exhibit cell‐to‐cell variability leading to signficant population heterogeneity. Far from being a nuisance, the ever‐present cellular noise acts as a rich source of excitation that propagates through a gene network, carrying its distinctive fingerprint. This presents a golden opportunity for network and parameter inference. We use single cell measurement techniques (e.g. flow cytometry, mRNA FISH, or time-lapse microscopy) to quantify the statistics of population variability over time, which we then use to infer a network model. To carry out the inference we use optimiziation, maximum likelihood, and Bayesian inference methods. The underlying methods use the the Chemical Master Equation or rely on efficient inference based on moment equations or stochastic simulations.
Inference based on the Master Equation
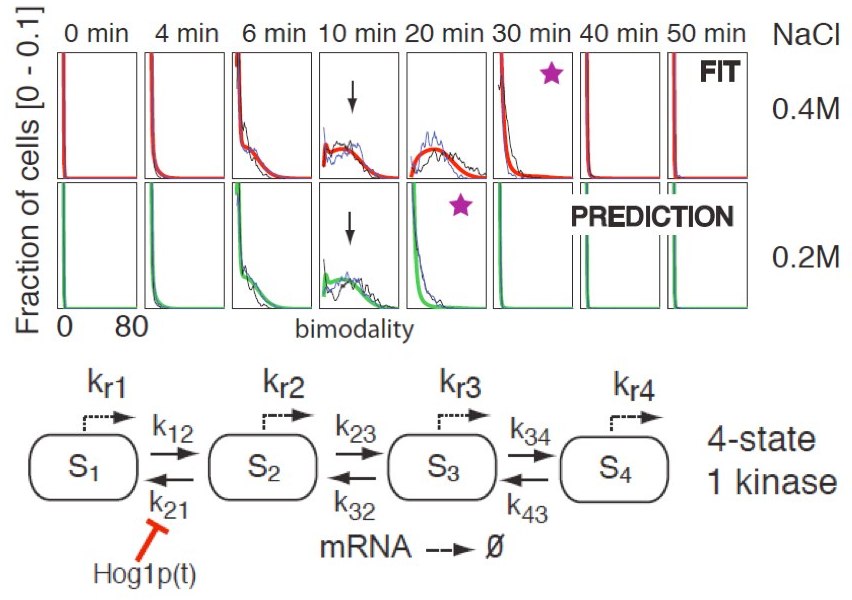
When the Chemical Master Equation can be effectively solved (or approximated using our Finite State Projection method), it can be used to carry out model inference. Single point estimates of the model parameters can be obtained through optimization that minimizes the norm of the difference between the model output and the measured data, or using a maximum likelihood approach. This has been shown to be very effective for inference of models of a stochastic toggle switch, a stochastic methylation based switch in E. coli, or the Hog pathway in yeast (using FISH mRNA).
Bayesian Inference Based on Monte Carlo Simulations
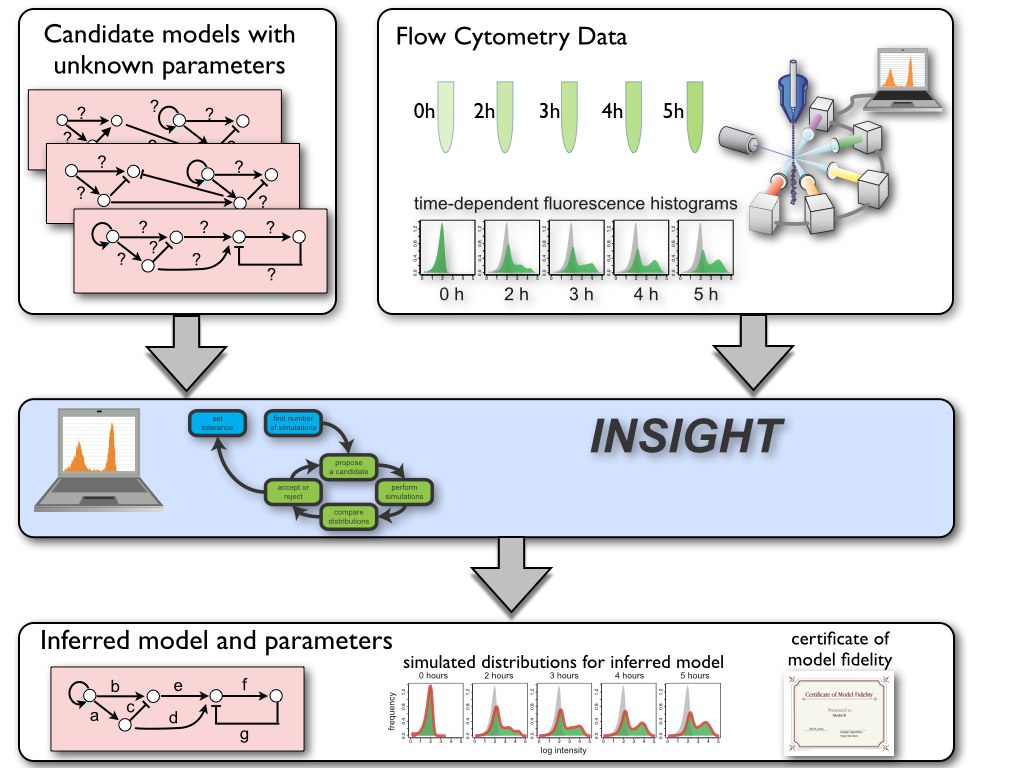
We have developed a novel method, called Inference for Networks of Stochastic Interactions among Genes using High-Throughput data (INSIGHT), for systematically combining high-throughput time-course single-cell distribution measurements with computer-generated stochastic simulations of candidate gene network models to infer the network’s stochastic model and its parameters. By exploiting the mathematical relationships between experimental and simulated population histograms, INSIGHT achieves scalability, efficiency and accuracy while entirely avoiding approximate stochastic methods.
G. Neuert, B. Munsky, R. Z. Tan, L. Teytelman, M. Khammash, and A. van Oudenaarden
"Systematic Identification of Signal-Activated Stochastic Gene Regulation," Science, 339 (6119), 584-587. external page DOI
G. Lillacci and M. Khammash
"The Signal within the Noise: Efficient Inference of Stochastic Gene Regulation Models using Fluorescence Histograms and Stochastic Simulations", Bioinformatics, 2013. external page DOI
G. Lillacci G. and M. Khammash
"A distribution-matching method for parameter estimation and model selection in computational biology,'' Int. J. Robust Nonlinear Control, 22: 1065–1081, 2012. external page DOI
Brian Munsky and Mustafa Khammash
"Identification from stochastic cell-to-cell variation: a genetic switch case study," IET Systems Biology, 4, No. 6, 356-366, 2010. external page DOI
G. Lillacci and Mustafa Khammash
"Parameter Estimation and Model Selection in Computational Biology," PLos Computational Biology, 6(3), e1000696, 2010. external page DOI
B. Munsky, B. Trinh, and M. Khammash
"Listening to the Noise: Random Fluctuations Reveal Gene Network Parameters," Molecular Systems Biology, EMBO/Nature, Vol. 5, p. 318, 2009. (Leon Heller Postdoctoral Publication Prize in Theoretical Physics) external page DOI
Hana El-Samad, Stephen Prajna, Antonis Papachristodoulou, John Doyle, and Mustafa Khammash
"Advanced Methods and Algorithms for Biological Networks Analysis,” Proceedings of the IEEE, Vol. 94, No. 4, April 2006. external page DOI